DTI







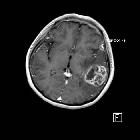

Diffusion tensor imaging (DTI) is an MRI technique that uses anisotropic diffusion to estimate the axonal (white matter) organization of the brain.
Fiber tractography (FT) is a 3D reconstruction technique to assess neural tracts using data collected by diffusion tensor imaging.
Diffusion-weighted imaging (DWI) is based on the measurement of thermal Brownian motion of water molecules. Within cerebral white matter, water molecules tend to diffuse more freely along the direction of axonal fascicles rather than across them. Such directional dependence of diffusivity is termed anisotropy. This direction of maximum diffusivity along the white-matter fibers is projected in the final image.
Clinical applications
For many, diffusion tensor imaging is synonymous with MR imaging of the CNS. However, its use for the assessment of highly-organized body systems outside the CNS, where anisotropy can facilitate early detection of pathology, has been gaining favor in recent years. Applications include:
- assessment of the deformation of white matter by tumors - deviation, infiltration, destruction of white matter
- delineation of the anatomy of immature brains
- pre-surgical planning
- Alzheimer disease - detection of early disease
- schizophrenia
- focal cortical dysplasia
- multiple sclerosis - plaque assessment
- early identification of musculoskeletal and peripheral nerve pathology
Quantitative analysis methods
- ROI (region of interest) based
- voxel-based
- histogram analysis
- tractography/fiber tracking
Physics of DTI
Some terms
- diffusion tensor imaging provides a quantitative analysis of the magnitude and directionality of water molecules
- the word tensor indicates the use of a 3x3 matrix with eigenvalues and eigenvectors as its constituents
- the two main parameters derived from DTI data are mean diffusivity (MD), also referred to as apparent diffusion coefficient (ADC), and fractional anisotropy (FA)
- FA reflects the directionality of molecular displacement by diffusion and varies between 0 (isotropic diffusion) and 1 (infinite anisotropic diffusion). FA value of CSF is 0
- MD reflects the average magnitude of molecular displacement by diffusion. The higher the MD value, the more isotropic the medium
- AD - axial diffusivity represents the longest eigenvector
- RD - radial diffusivity represents the average of two shorter eigenvectors
- DTI data acquisition is done by SE-EPI with the application of diffusion gradients in multiple directions (SE-EPI = spin-echo echo-planar imaging, using pairs of 90-180 degree pulses, giving T2-weighting)
Color coding
In fiber tractography imaging, the convention for color coding is a follows:
- red: transverse fibers
- green: anteroposterior fibers
- blue: craniocaudal fibers
Fibers with oblique orientation are represented with colors originating from the combination of the three primary colors:
- Red + blue = magenta;
- Green + red = yellow;
- Green + blue = cyan
Limitations of the fiber tractography
The rational of the tractographic algorithms lies in the presupposition that in each voxel, the direction of the main eigenvector coincides with the average direction of a single fiber bundle. The approach, therefore, leads to a correct result only if the region of interest is homogeneous and, the direction variations of the fasciculi are of the order of size of the voxels. It follows that where more bundles of fibers coexist or where they cross, approach, converge or diverge, the algorithm works poorly. These limits, in clinical practice, could lead to following paths that do not exist (false positive) or to not adequately follow paths that exist (false negative); therefore, the interpretation of tractographic reconstructions requires prior experience and knowledge.
Other limitations include, the inability of the algorithm to distinguish the direction of the neural pathway (afferent from efferent projections), to determine its function and to identify the presence of synapses along the course of the same neural pathway.
Siehe auch:

 Assoziationen und Differentialdiagnosen zu Diffusions-Tensor-Bildgebung:
Assoziationen und Differentialdiagnosen zu Diffusions-Tensor-Bildgebung:
