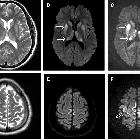
Diffusion-weighted imaging
Diffusion-weighted imaging (DWI) is a form of MR imaging based upon measuring the random Brownian motion of water molecules within a voxel of tissue. In general simplified terms, highly cellular tissues or those with cellular swelling exhibit lower diffusion coefficients. Diffusion is particularly useful in tumor characterization and cerebral ischemia.
Terminology
A great deal of confusion exists in the way the clinicians and radiologists refer to diffusion restriction, with both groups often appearing to not actually understand what they are referring to.
The first problem is that the term "diffusion-weighted imaging" is used to denote a number of different things:
- isotropic diffusion map (what most radiologists and clinicians will refer to as DWI)
- the pulse sequence that results in the generation of the various images (e.g. isotropic map, b=0, ADC)
- a more general term to encompass all diffusion techniques including diffusion tensor imaging
Additionally, confusion also exists in how to refer to abnormal restricted diffusion. This largely stems from the initial popularisation of DWI in stroke, which presented infarcted tissue as high signal on isotropic maps and described it merely as "restricted diffusion", implying that the rest of the brain did not demonstrate restricted diffusion, which is clearly not true. Unfortunately, this shorthand is appealing and is more widespread than using the more accurate but clumsier "diffusion demonstrates greater restriction than one would expect for this tissue."
To make matters worse, many are not aware of the concept of T2 shine-through, a cause of artifactual high signal on isotropic maps, or interpret it as a binary feature with T2 contribution to signal either present or absent when in reality there is always a T2 component even to regions with true T2 diffusion restriction.
A much safer and more accurate way of referring to diffusion restriction is to remember that we are referring to actual apparent diffusion coefficient (ADC) values, and to use wording such as "the region demonstrates abnormally low ADC values (abnormal diffusion restriction)" or even "high signal on isotropic images (DWI) is confirmed by ADC maps to represent abnormal restricted diffusion".
Physics
As opposed to essentially free diffusion of water kept inside a container, diffusion of water inside brain tissue, for example, is hindered primarily by cell membrane boundaries. The overall diffusion characteristics of a single volume represent the combined water diffusion in a number of compartments:
- diffusion within the intracellular fluid
- within the cytoplasm generally
- within organelles
- diffusion within extracellular fluid
- interstitial fluid
- intravascular
- lymph
- various biological cavities, e.g. ventricles of the brain
- diffusion between intra- and extracellular compartments
The contribution of each one of these will depend on the tissue and pathology. For example, in acute cerebral infarction it is believed that the decrease in ADC values is the result of a combination of water moving into the intracellular compartment (where its diffusion is more impeded by organelles than it is in the extracellular space) and the resulting cellular swelling narrowing the extracellular space . Similar mechanisms result in low ADC values in highly cellular tumors (e.g. small round blue cell tumors (e.g. lymphoma/PNET) and high grade gliomas (GBM)).
The further an individual water molecule diffuses during the sequence the more it will be exposed to varying gradient strength and the more it will be dephased reducing the amount of signal returned. This occurs at a much smaller scale than a single voxel. The strength of this effect (in other words how much the signal will be attenuated by diffusion) is determined by the b value.
Clinical application
Diffusion-weighted imaging has a major role in the following clinical situations :
- early identification of ischemic stroke
- differentiation of acute from chronic stroke
- differentiation of acute stroke from other stroke mimics
- differentiation of epidermoid cyst from an arachnoid cyst
- differentiation of abscess from necrotic tumors
- assessment of cortical lesions in Creutzfeldt-Jakob disease (CJD)
- differentiation of herpes encephalitis from diffuse temporal gliomas
- assessment of the extent of diffuse axonal injury
- grading of diffuse gliomas and meningiomas
- assessment of active demyelination
- grading of prostate lesions (see PIRADS)
- differentiation between cholesteatoma and otitis media
MRI sequence
A variety of techniques for generating diffusion maps have been developed. By far the most commonly used technique relies on a spin-echo echo-planar sequence (SE-EPI) although non-EPI techniques (e.g. turbo spin-echo) are also available and are of use particularly where tissue is adjacent or within bone where T2* effects cause artifact, distortion and signal loss on EPI sequences .
General principle of diffusion-weighted imaging
The fundamental idea behind diffusion-weighted imaging is the attenuation of T2* signal based on how easily water molecules are able to diffuse in that region. The more easily water can diffuse (i.e. the further a water molecule can move around during the sequence) the less initial T2* signal will remain. For example, water within cerebrospinal fluid (CSF) can diffuse very easily, so very little signal remains and the ventricles appear black. In contrast, water within brain parenchyma cannot move as easily due to cell membranes getting in the way and therefore the initial T2* signal of the brain is only somewhat attenuated. An important consequence of this is that if a region of the brain has zero T2* signal it cannot, regardless of the diffusion characteristics of that tissue, show signal on isotropic diffusion-weighted images.
The way in which diffusion information is extracted from the tissue is to first obtain a T2* weighted image with no diffusion attenuation. This is known as the b=0 image.
Next, the ease with which water can diffuse is assessed in various directions; the minimum is 3 orthogonal directions (X, Y and Z) and we will use this for the rest of this explanation.
This is done by applying a strong gradient symmetrically on either side of the 180-degree pulse. The degree of diffusion weighting is dependent primarily on the area under the diffusion gradients (which is in turn related to the amplitude and duration of the gradient) and on the interval between the gradients. The combination of these factors generates the b value. The higher the number the more pronounced the diffusion-related signal attenuation.
Stationary water molecules acquire phase information by the application of the first gradient. After the 180-degree pulse, however, they are exposed to the exact same gradient (because they have not changed location) which undoes all the effects of the first (since they have flipped 180-degrees). Hence at the time the echo is generated they have retained their signal.
Moving water molecules, on the other hand, acquire phase information by the first gradient but as they are moving when they are exposed to the second gradient they are not in the same location and thus are not exposed to precisely the same gradient after the 180-degree pulse. Hence they are not rephased and they lose some of their signal. The further they are able to move the less successfully they will be rephased and the less signal will remain.
Generating isotropic DWI and ADC maps
The aforementioned process generates four sets of images: a T2* b=0 image and three diffusion-weighted images (one for each X, Y and Z direction) with the T2* signal attenuated according to how easily water can diffuse in that direction.
These images can then be combined arithmetically to generate maps that are devoid of directional information (isotropic): isotropic diffusion-weighted images (what we usually refer to as DWI) and ADC maps.
To generate the isotropic DWI maps, the geometric mean of the direction-specific images is calculated.
The ADC map, in contrast, is related to the natural logarithm (ln) of the isotropic DWI divided by the initial T2* signal (b=0). These can either be calculated directly from the isotropic DWI images or by finding the arithmetic mean of ADC values generated from each directional diffusion map.
See also
- b values
- apparent diffusion coefficient
- diffusion tensor imaging
- diffusion weighted MRI in acute stroke
- restricted diffusion in the basal ganglia
- intracranial lesions which show restricted diffusion
Siehe auch:
- Arachnoidalzyste
- MR Pulse Sequenzen - Abkürzungen
- Ischämischer Schlaganfall
- diffusion weighted MRI in acute stroke
- Diffuses axonales Schädelhirntrauma
- epidermale Inklusionszyste
- Herpesenzephalitis
- ADC abnormality of the basal ganglia
- Creutzfeldt-Jakob-Krankheit
- Diffusions-Tensor-Bildgebung
und weiter:

 Assoziationen und Differentialdiagnosen zu diffusionsgewichtete Bildgebung:
Assoziationen und Differentialdiagnosen zu diffusionsgewichtete Bildgebung: